Update: Before I get any further, I'd like to mention that the 2012 Open data I am using is from Jeff King, downloaded from http://media.jsza.com/CFOpen2012-wk5.zip. Thanks a ton to Jeff for gathering all the data. Much of this analysis would not be possible without it.
First, let me lay out four key flaws I see in the points-per-place system:
1) The results are heavily dependent on who you include in the field. Take the Games competitors, for example, and rank them based on their Open performance. You get very different results if you score each event based on the athletes' rank among the entire Open field than if you score each event based on the athletes' rank among only the Games competitors. Neal Maddox would move from 5th using the entire field to 2nd using only Games competitors, Rob Forte would move from 15th to 25th and Marcus Hendren would move from 34th to 16th. This is a problem.
2) There is no reward for truly outstanding performances. In the Open, Scott Panchik did 161 burpees in 7 minutes. The next closest mens Games competitor was Rich Froning at 141. In a field with only Games competitors, Panchik would only gain ONE point on Rich. He was not rewarded at all for any burpees beyond 142 (even with all Games competitors included, he only beat Froning by 33 spots, a relatively slim margin among 30,000+ competitors).
3) Along the same lines, tiny increments can be worth massive points if the field is bunched in one spot or another. If I had performed one more burpee (I did 104), for instance, I would have gained 857 spots worldwide. The difference between 70 and 71 burpees (a larger proportional increase in work output) was worth only 327 spots. And the gap between 141 and 161 was only 33 spots.
4) Other athletes can have a huge impact on the outcome between two competitors. Why should the differential between Rich Froning and Graham Holmberg come down to how many other competitors finished between their scores on a certain event? If those other competitors hadn't even been competing, it wouldn't change how Rich and Graham compared to each other.
Now, while I don't agree with everything Tony Budding says, I think he brought up a good point when he defended the scoring system on the CrossFit Games Update show earlier this year. Regardless of whether it has some mathematical imperfections, the fact of the matter is the points-per-rank scoring system is very easy to understand and very easy to implement. Watching the Olympic Decathlon, which has been refining its scoring system for years, reminded me why the points-per-place system isn't so bad. Unless you have a scoring table and a calculator handy, the Decathlon scores seem awfully mysterious. So if we're going to come up with a scoring system to replace the points-per-place system, I believe it has to be easy for viewers and athletes to understand.
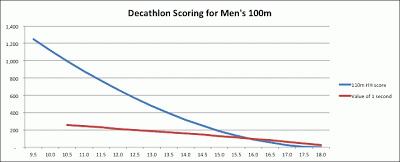
That being said, we can learn from what the Decathlon has done. The idea behind the Decathlon scoring system is to attempt to weight each of the events equally, so that performances of equal skill level in each event yield similar point totals. Beyond that, the same scoring system should be applicable to athletes ranging from beginners to elite athlete. Additionally, the scoring system for all events is at least slightly "progressive" - this means that as performances get closer and closer to world record levels, each increment of performance more and more valuable. For instance, the difference in score between a 11-second to a 12-second 100 meters is wider than the difference between a 12-second and a 13-second 100 meters.
Each event is scored based on a formula, taking one of two forms
Points for running events = a * (b - Time)^c
Points for throws/jumps = a * (Distance - b)^c
For each, the value of b represents a beginner level result (for instance, 18.00 seconds in the men's 100 meters), and c is greater than 1, which is the reason the scores are progressive. Certain events are more progressive than others; generally, the running events are more progressive than the throws. Here is a chart showing the point value of times in the 100 meters.
The Decathlon scoring system, for all its complexity, generally does a good job distributing points among the 10 events. It also rewards exceptional performances much more so than the points-per-place system we use in CrossFit. However, there is simply no way to create such a system for CrossFit, even if we were fine with the complexity. Why? Because the events are unknown, and they almost always have never been performed before in competition, which means calibrating the formulas to be appropriate would have to be done on the fly. There was no objective measure about what a "good" performance was on the Track Triplet before it occurred this year's Games, and there certainly was no way to say what was an equivalent performance on the Medball Clean-HSPU workout, for example.
Of course, it's easy to pick apart other scoring methods, but the key question here is whether we can come up with anything better. In thinking about this post, I initially considered three types of systems: 1) a logarithm system, in which all performances are converted to logarithms, which gives us an indication of scores relative to one another; 2) a percentage of work system, where the top finisher is awarded a score of 100% and all others are scored based on their performance relative to that performance; and 3) a standard deviation system, where each finisher's score is based on how far from the average score they fell.
As we move away from a points-per-place system, there is one key point that need to be addressed. Since we are now considering differences in performance rather than just rank, we must think about how much a repetition of one movement is worth compared to a repetition of another movement. Think of Open WOD 4: one muscle-up is far more difficult than one double-under. If we count each movement equally, an athlete who completes ten muscle-up scores 250, which is only 4.2% higher than an athlete who completes all the double-unders but no muscle-ups (240). Clearly, this does not accurately reflect the difference in performance, and the movements need to be weighted accordingly. I think that it would not be too difficult for those designing the workout to make the points-per-rep system clear when the workout is announced. For example, HQ could simply say that each segment of the workout is weighted equally; completing 150 wall-balls is worth one point, completing 90 double-unders is worth one point and completing 30 muscle-ups is one point (10 muscle-ups is then worth 0.33 points). That's still a little light on the muscle-ups, in my opinion, but it is a simple solution for now, and it works well for most workouts (I'll use it for most events in my comparisons throughout this post). HQ could come up with whatever weightings they feel are appropriate. Sure, they would be somewhat arbitrary, but the workouts themselves are also arbitrary; if HQ lays out the rules, people will play by them.
Now, let me first discuss the logarithm system, which is definitely the most unusual of the three. The key point about logarithms, in this context, is that the difference in two athletes' scores is based only on the ratio of their performances. For example, let's say we had 3 athletes, one of which completed 40 burpees, one of which completed 80 burpees and one of which completed 160 burpees. The logarithm scoring system (we'll use a natural logarithm, although the base is irrelevant) would give athlete A a score of 3.689, athlete B a score of 4.382 and athlete C a score of 5.075. The difference between athletes A and B is .693, which is exactly the same as the difference between athletes B and C. By using this system, we can compare a 20-minute event exactly as we'd compare a 5-minute event: it's only the ratio between athletes that is important. The scores are also completely independent of who is in the field.
However, the logarithm system has a couple of significant drawbacks. First, it is certainly not easy to interpret, and most non-math majors might have a tough time recalling what a logarithm even is. But more importantly, this system does not reward the outstanding scores whatsoever. It actually does the reverse of the Decathlon's progressive system: as scores get better, you need a wider and wider gap in performance to gain the same point value. Scott Panchik's 161 burpees would give him the same point advantage over Rich Froning's 141 as an athlete doing 40 burpees would gain on an athlete doing 35.
So as mathematically pleasing as it is, let's drop the logarithm from the discussion. Let's move on to the percentage of work method. This method is simple: to score an athlete, we simply take the ratio of their score to the top score in competition (personally, I'd keep the genders separate). My score of 104 burpees would be translated to a score of 64.6% (104/161). Using this system, here are the top 5 men's Open results among competitors who reached the Games:
Note: In calculating the scores for each workout, I assumed each portion of workouts 3 and 4 were weighted equally (for WOD 3, 15 box jumps = 12 push press = 9 toes-to-bar = 1.00 points each). For workout 2, I weighted each rep by the weight used. The first 30 reps were worth 75 points each, then 135 each for the next 30, and so on. Workouts 1 and 5 were scored with all reps counting equally.
Keep in mind that for workouts with a set workload performed for time, we need to convert the times to work-per-unit of time. For instance, doing Fran in 4:00 could be converted to 90 reps/240 seconds = 0.375. A 5:00 Fran would be 0.300, which would be 80% of the work (well, technically power, not work) of the 4:00 Fran. If we have an event where all athletes might not finish within a time cap, we need to be careful to weight the reps appropriately (as described above). For instance, if Open WOD 4 had been prescribed as 150 wall-balls, 90 double-unders, 30 muscle-ups for time (12:00 time cap), we use our weights to accurately score all those athletes who did not finish in 12:00.
This method solves many of the issues we had with the points-per-place system. The only part of the scoring system that is dependent on the rest of the field is the winner, and most fields of competitors will have a winning score that is the same ballpark for a given workout. If you were to restrict the field to only Games competitors, the results would be identical. Outstanding performances are indeed rewarded, like Scott Panchik's 161 burpees (12% spread over next highest Games athlete). Bunching in one spot is not an issue, because athletes are scored based on performance only, not rank. Similarly, other competitors finishing between two athletes has no bearing on the relative scores of those two athletes.
However, there is one major concern about the percentage-of-work system. This method assumes that the athletes' scores will be distributed between 0 and the top score in a similar fashion for each workout, when in reality, some events are naturally going to have a tighter pack. Consider the sprint workout at the Games: the last-place competitor on the men's side would have received a score of 78%. On the medball clean-HSPU workout, the last-place competitor would have scored just 30%. Essentially, the sprint workout becomes much less meaningful than the medball clean-HSPU workout because there is much less opportunity for the winners to gain ground. This is easy to see when we compare the distributions of the two workouts graphically.
There are a couple of options to remedy this. One option is to modify the percentage-of-work system so that we see where an athlete's percentage of work falls between the lowest and highest score. Using this method, the 30% on the medball clean-HSPU workout and the 77% on the sprint both receive a score of 0%. A score of 65% on the medball clean-HSPU would score 50%, as would an 89% on the sprint workout. The problem with this solution is that one outlier performance can skew the low end. In the Open, using the entire field, there was a score of exactly 1 on every workout. Even among Games competitors, there may be one athlete who either is injured or simply struggles mightily with a particular movement, and that can drag the low end down unfairly.
The second option is to use the standard deviation system. This system looks at how far an athlete was from the average score in a given workout, taking into account how spread out the scores are. To calculate an athlete's score, we use the following formula:
Score = (Athlete's Result - Average Result) / Standard Deviation
For those unfamiliar with a standard deviation, it basically gives an indication of how far in either direction most athletes were from the average. If a distribution is normal (which most of these workouts tend to be), then in general, about 2/3 of the scores will fall within 1 standard deviation of the average. About 95% will fall within 2 standard deviations of the average. A related concept, called the coefficient of variation, tells us how large the standard deviation is compared to the mean (which basically indicates whether we had a tight pack or a more spread out field). The coefficient of variation for the sprint was 4.9%, but on the medball clean-HSPU event it was 28.8%.
On the sprint event, the average result was 6.59 meters/second (45.53 seconds). The winning speed was 7.14 meters/second (42.00) seconds. The standard deviation was 0.32, so the winning time would receive a score of (7.14 - 6.59) / 0.32 = 1.73. The worst time (5.51 meters/second, or 54.40 seconds) would receive a score of -3.36, giving us a total spread of 5.09. On the medball clean-HSPU event, the winning speed was 0.96 stations/minute (finished in 6:15.8). The standard deviation was 0.18, so the winning time would receive a score of 1.98. The worst time (0.29 stations/minute, or 10:00 plus 25 reps remaining) would receive a score of -1.83, giving us a total spread of 3.81, which is actually considerably less than the spread on the sprint workout. The reason is that the score of 54 seconds in the sprint was well outside the normal range, and it was punished accordingly.
Update: Using the standard deviation system (with all Games competitors included in calculating mean and standard deviation), here are the top 5 men's Open results among competitors who reached the Games:
Mathematically, the biggest drawback to this system is that it is somewhat dependent on the field. On Open WOD 1, the overall average score was 95.4 (among men under 55 years old) with a standard deviation of 17.2. If we limit that to only Games competitors, the average is 123.8 and the standard deviation is only 8.8. This makes an outlier performance like Panchik's 161 burpees more valuable when we only look at Games competitors than if we look at the whole field. Still, each competitor moved an average of just 1.3 spots in either direction when we switched the field from all Open competitors to Games competitors only. Using the points-per-place system, each competitor moved an average of 3.5 spots.
My feeling is that, despite this drawback, the standard deviation system is the optimal solution. I understand that the term "standard deviation" may sound foreign to many athletes and fans, but it is a relatively simple and intuitive mathematical concept. And we can easily change the name to something less intimidating, perhaps the "spread factor" or simply the "spread." If the weighting of each movement is clearly defined beforehand, the calculations for the scores of each workout should not be overly difficult, and the results should be fairly easy to understand. Certainly it would be far more transparent than the Decathlon system, while providing a similar level of fairness. There is also the convenient property that a total score of 0.00 is exactly average.
Imagine competing in the Open with this system. Once you have completed your workout, assuming there have been at least a few thousand entries so far, you already have a reasonably good idea of your score. The average and the standard deviation will not change much over the course of the next couple days. You won't need to worry about a logjam at one particular score unduly influencing your own result. The effects of attrition (fewer people completing the workout each week) should be basically negated, since we are not scoring based on points.
In my view, this is a much more equitable Open. It also makes for a more equitable Regional and Games competition. Does that mean HQ will veer from their hard-line stance on the points-per-place system? I have my doubts. But hopefully this provides some insight into why this is a discussion worth having.